V ↗kvantitativní lingvistice se používá při analýzách textu a označuje stupeň diverzifikovanosti sledovaných jednotek (syntagmat, slovních tvarů, lemmat, morfů, slabik, fonémů, hlásek atp.). Čím je e. vyšší, tím je vyrovnanější poměr daných jednotek v textu, nízká e. je naopak projevem vysoké koncentrace, kdy několik málo jednotek se vyskytuje s výrazně vyšší frekvencí.

Do lingvistiky byl pojem e. zaveden z teorie informace. Přestože existuje množství různých definic e. (srov. ✍Esteban & Morales, 1995), v lingvistice se zpravidla používá pojetí ✍Shanonna (1948), který ji definoval jako

,

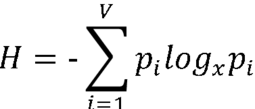kde p_i je pravděpodobnost dané jednotky v textu, log_x je logaritmus o základu x (zpravidla se používá binární logaritmus o základu x = 2 n. přirozený logaritmus o základu x = e, kde e ≈ 2,718 je Eulerovo číslo) a V je počet různých jednotek (typů). Pravděpodobnost p_i se odhaduje prostřednictvím relativní frekvence, tj.

,

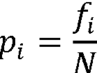kde f_i je frekvence jednotky v textu a N počet všech jednotek (tokenů). Původní vzorec lze tak zapsat jako

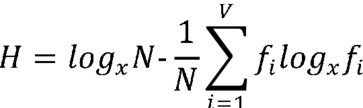
Minimální míra entropie H_min = 0 by nastala v případě, že by text byl tvořen jedinou jednotkou, která by se neustále opakovala. Naopak maximální entropii by měl text, ve kterém by se všechny jednotky vyskytovaly se stejnou frekvencí:

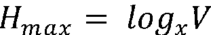
Míra e. textu se pohybuje v intervalu <0, log_xV>, její hodnotu tedy významně ovlivňuje počet různých jednotek (typů) v textu. V případě analýzy entropie založené na frekvenci jednotek s velkým inventářem, jako jsou slovní tvary, lemmata, slabiky či morfy, je počet různých jednotek v textu závislý na jeho délce, tudíž je na délce textu závislá i hodnota maximální entropie H_max (k vlivu délky textu viz ↗slovní bohatství textu). To znamená, že je neadekvátní porovnávat texty o různé délce a je nutné buď

(a) text segmentovat na stejné délkové úseky (např. 100 jednotek), v každému úseku zjistit entropii a následně vypočítat průměrnou hodnotu entropie 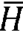, tj.

,

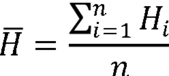kde H_i je entropie daného úseku a n je počet těchto úseků v textu, n.

(b) pracovat s relativní hodnotu entropie H_rel, která je definována jako poměr empirické entropie H vzhledem k jejímu maximu, tj.

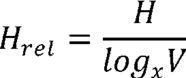
V případě analýzy e. založené na frekvenci jednotek s relativně malým inventářem – v jazyce jde zřejmě jen o hlásky či fonémy (je však možné pracovat také s kategoriemi, jako je gramatický pád, slovní druh, sémantická role, větný člen atp.) – dojde v textu (pokud je dostatečně dlouhý) ke stavu, kdy se v něm realizuje celý inventář sledovaných jednotek. Od toho stavu již délka textu nehraje roli, a je proto možné porovnávat texty různé délky.

Rozdíly mezi hodnotami entropie H lze v dostatečně dlouhých textech statisticky testovat prostřednictvím asymptotického testu

,

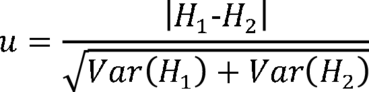kde H₁ a H₂ jsou entropie dvou různých textů a Var(H) je rozptyl, jenž ✍Popescu & Vidya ad. (2009:184) ho definují

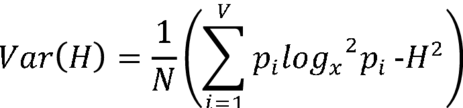
E. slovních tvarů či lemmat v textu je možné interpretovat ve vztahu k ↗slovnímu bohatství textu, e. hlásek ve verši ve vztahu k eufonii, e. slabik k průměrné délce slova v jazyce, e. fonémů k míře jejich redundance ve slovech atd. E. se také používá v numerické estetice (✍Bartók & Janoušek, 1980; ✍Birkhoff, 1933; ✍Moles, 1968; ✍Rigau & Feixas ad., 2007). Obecně lze říct, že e. je jedním ze způsobů, jak charakterizovat distribuci zvolených jednotek v textu či jazyce.